『情報と秩序』を読みました。
『市場の秩序と無秩序についてです』の記事で秩序について考えました。 『情報と秩序』の内容をもとに、もう少しだけ秩序について考えてみました。
ボルツマンの定義
ボルツマンとシャノンのエントロピーの定義の違いを理解するため、半分座席の埋まったスタジアムを考えてみよう。 半分座席の埋まったスタジアムには、ある重要な特徴がある。 座席の埋まり方にさまざまな組み合わせがありうる、という点だ。 その組み合わせについて考察すれば、エントロピーの意味が説明できる。
まず、人々が自由に席を移動できるケースを考えてみる。 この場合、半分座席の埋まった状態として、座席の上半分を空席にし、全員がフィールド側に寄り固まるケースが考えられる。 もうひとつ考えられるのは、下半分を空席にし、全員がフィールド側から遠い側に寄り固まるケース。 また、人々がランダムな座席に座るケースも考えられるだろう。
さて、このスタジアムの例を用いてエントロピーを説明するため、あとふたつ概念を導入しておこう。 ひとつめに、スタジアムに座っている人々の一つひとつの配置のことを、その系の「状態」(正確には「微視的状態」と呼ぶ)。 ふたつめに、何らかの尺度を用いて、同等な配置というものを特定できると仮定する。 この例でいえば、「埋まっている座席の列番号の平均」という単純な尺度でもかまわない。
この例の場合、エントロピーの統計物理学的な定義は、同等なすべての状態の数の割合である(厳密にいうとその「対数」だが、私が言おうとしている点にとってはあまり重要でない)。 したがって、エントロピーが最小になるのは、全員がフィールド側またはその反対側に固まっている場合だ。 そのように座る方法は、ただ一通りしかないからだ。 エントロピーが最大になるのは、埋まっている座席の列番号の平均がちょうど真ん中の列である場合だ。 埋まっている座席の列番号の平均がちょうど真ん中の列になるような座り方はたくさんあるからだ。 ボルツマンの定義では、エントロピーとは同等な状態の「多重度」である。 スタジアムの例の場合、同等な状態の数が最大になるのは、埋まっている座席の列番号の平均がちょうど真ん中の列になる場合だ。
情報と秩序 第2章 無意味の実体
ボルツマンの定義では同等な状態の「多重度」のことをエントロピーというみたいです。
この例にあるような図を作って確認していくことにしました。 最初に x 軸に 10 個、 y 軸に 10 個、合計 100 個の点がある図を作りました。

ここに 50 個の点を埋めていきます。
エントロピーが最小
エントロピーが最小になるケースの図を作りました。
下半分を埋めたケースです。

「埋まっている点の y 軸の値の平均」が 2 になりました。
上半分を埋めたケースです。

「埋まっている点の y 軸の値の平均」が 7 になりました。
「埋まっている点の y 軸の値の平均」が 2 になるのも、 7 になるのも、上の図の配置以外にありません。 それぞれ 1 つだけなので、「多重」ではありません。 こういうのをエントロピーが最小というみたいです。
エントロピーが最大
エントロピーが最大になるケースの図をいくつか作りました。
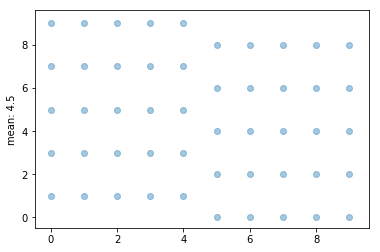


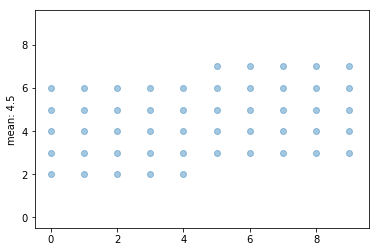
4 つだけ載せてみました。 どれも「埋まっている点の y 軸の値の平均」が 4.5 になっています。 組み合わせがたくさんありそうで、全部は確認していませんけれども…(いくつあるんだろう?)。 少なくとも「エントロピーが最小」のところで挙げた 2 と 7 よりは 4.5 の方が多重度が高いです。 ここに挙げただけでも、もうすでに同等な状態が 4 つはあるわけですし。
ランダム
ランダムに点を埋めた図を作ってみました。
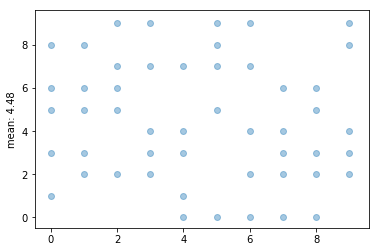
「埋まっている点の y 軸の値の平均」が 4.48 でした。 4.5 に近いのでエントロピーが大きい方だと言えるんじゃないかと思います。
市場
ここから市場に置き換えて考えてみました。 前提として次のような認識を持っていました。
- エントロピーが最小=秩序=トレードするところ
- エントロピーが最大=無秩序=トレードしてはいけないところ
エントロピーが最小の図から考えてみます。
「埋まっている点の y 軸の値の平均」が 2 の図は下半分の点が埋まっていました。 下なので売りに偏っている、とでも見たら良いのでしょうか。 そうだとすると「トレードするところ」と認識していても良さそうです。
「埋まっている点の y 軸の値の平均」が 7 の図は上半分の点が埋まっていました。 上なので買いに偏っている、とでも見たら良いのでしょうか。 そうだとすると「トレードするところ」と認識していても良さそうです。
同等な状態の数が 1 つなので、不確実ではなくて確実とも言えると思います。 確実なところでトレードした方がいいというのも納得できる理由です。
エントロピーが最大の図は難しそうなので置いておいて、先にランダムな図を考えてみます。
エントロピーが最大ではないですが、大きくて、ぱっと見でも無秩序そうに見えます(主観的すぎますか?)。 上にも下にも点がまばらにあるので、買いも売りも入り混じっている、とでも見たら良いのでしょうか。 そうだとすると「トレードしてはいけないところ」と認識していても良さそうです。
同等な状態の数がたくさんあるので、確実ではなくて不確実とも言えると思います。 不確実なところではトレードしない方がいいというのも納得できる理由です。
最後に、エントロピーが最大の図を考えてみます。
上にも下にも点があって、買いも売りも入り混じっている、と見える…かもしれません。 同等な状態の数がたくさんあるので、確実ではなくて不確実とも言える…かもしれません。 ここまで書いてきたような認識の流れなら…。 でも、この記事に載せた 4 つの図は、ぱっと見、無秩序そうには見えないんです(主観的すぎますか?) 整然としていて、規則正しくありそうに見えます。 これら(「整然」「規則」「一貫性」)は、『市場の秩序と無秩序についてです』の記事で『複雑で単純な世界』の中から秩序と無秩序を整理したときに出てきた単語です。
念のため述べておくと、エントロピーと聞いて無秩序を連想する人も多いと思うが、エントロピーは必ずしも無秩序の尺度ではない。 エントロピーはある状態の多重度(同等な状態の数)を測るものである。 ただし、無秩序な状態というのは多重度が高いことが多い。 したがって、現実には、エントロピーの高い状態というのは無秩序である可能性がきわめて高い。 そのため、無秩序とエントロピーを同一視するのは、あながち悪い単純化とはいえない。 ただ、無秩序が増大しなくてもエントロピーが増大するケースもありうる。 たとえば、箱の大きさが二倍になったときの気体の拡散について考えてみよう(スタジアムのサイズが二倍になったときの人々の拡散でもいい)。 この気体のエントロピーは、箱の大きさとともに増加する。 箱が大きければ大きいほど、気体の粒子の可能な配列方法は増えるからだ。 ところが、小さな箱よりも大きな箱のなかの気体のほうが無秩序だ、とはいえない。
情報と秩序 第2章 無意味の実体
どうやら必ずしも「エントロピーが最大=無秩序」ということではないみたいでした。 言葉の定義って難しい…。
この記事に載せた 4 つの図は、エントロピーが最大ではあるものの無秩序ではない、と言ってもいいのかなあ。 整然としていて、規則正しい、と言ってもいいのかなあ。 一貫性があって、予測が可能そう、と言ってもいいのかなあ。 そして、トレードをしてもいい、のかなあ。
終わり
つまり、シャノンの用語でいえば、情報とエントロピーは機能的に同等ということになる。
情報と秩序 第2章 無意味の実体
この記事ではボルツマンの定義のエントロピーを確認してみました。 けれども、エントロピーの定義はそれだけではないようです。
何か知ると、何か知らないことが増えます…。
作った図が含まれている Jupyter Notebook のファイルを Gist にアップロードしておきました。
最後に、著者の確立した「経済複雑性」という指標は興味深いです。
このプロセスの結果として、私が二〇〇八年に確立したのが、「経済複雑性(economic complexity)」という指標だ。 あとで説明するとおり、この指標の特徴は、将来の経済成長をかなり正確に予測できるという点だ。
情報と秩序 第10章 第六の物質
OEC: 経済複雑性の観測 から見ることができるみたいです。
