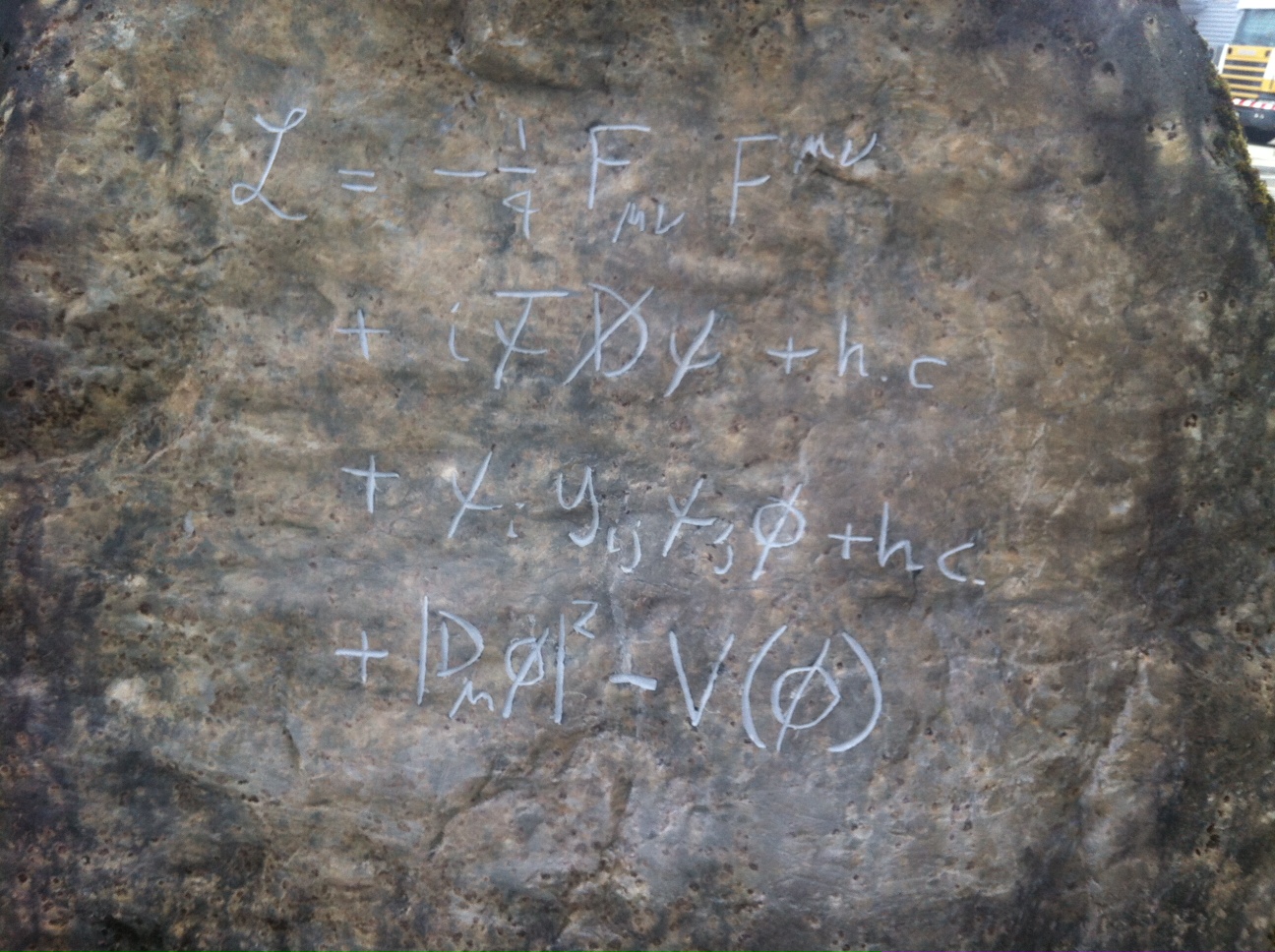素粒子の標準理論についての書き起こしをしてみました。
Prologue
1本の鉛筆を、尖った方を下にして机に立ててみてください。 もし、完璧に垂直に立てることができれば、バランスが取れて倒れないようにできるかもしれません。 だから、とにかく真っ直ぐに、垂直にして・・ あー、やっぱりダメですよねー。 どんなに真っ直ぐ立てても、鉛筆は必ず倒れてしまいます。 何度やっても、どれだけ完璧に垂直にしたとしても。 「そんなの当たり前じゃないか。」 とお思いになるかもしれません。 けれど、鉛筆が倒れるなんでもない現象が、ある科学的大発見の、大元になっていることをご存知でしょうか。 スイスにあるヨーロッパ合同原子核研究機構CERN(スイス)。 2012年7月。 ここで、一つの素粒子が発見されたという発表がありました。
私たちはついに 新しい素粒子を発見しました
ヒッグス粒子だと思います
ヨーロッパ合同原子核研究機構CERN
ヒッグス粒子。 この名前を聞いたことがある人もいるかもしれません。 人類が探し求めてきた最後の素粒子の発見として、最先端科学に馴染みのない人たちまでが湧いた、世紀の大発見と言われました。
私たちはこの世界が何から作られているのかを追い求め、宇宙のかなりの部分を理解できるようになりました。 ヒッグス粒子は見つけるべき最後のピースでした。 一つの時代が終わったと言えるでしょう。
1979年 ノーベル物理学賞 シェルドン・グラショウ
でも、一体なぜ、人類が追い求めてきた素粒子が、倒れる鉛筆と関係があるというのでしょう。 鉛筆が倒れる現象の重要さに、世界で始めて気付いたのは、ある日本人物理学者でした。 2008年のノーベル賞を受賞した、南部陽一郎。 92歳。 南部は、物理学の最終目標と言われる、ある研究を長年続けてきた一人でした。 この世に、もし創造主がいるとしたなら、一体どんな設計図に基づいて、宇宙を作り上げたのか。 アインシュタイン以来、物理学者たちは、いわば神の設計図を発見し、それを数学の言葉、数式で書き表したいと血眼になってきました。 神の数式の探求です。
物理をやりだした以上は そういうこと(究極理論)をやりたいと
つまり なんでも分かりたいという
分かるはずだ 分かりたいという欲望ですよね
2008年 ノーベル物理学賞 南部陽一郎
これまでも物理学者たちは、いろいろな現象を数式で表すことに、一応の成功を収めてはきました。 例えば、オーロラが輝く理由は、だいたいこんな数式で表せます。
$$ \nu \sim R \left( \frac{ 1 }{ n ^ { 2 } } - \frac{ 1 }{ m ^ { 2 } } \right) $$
大気の動きならこんな数式。
$$ \rho \frac{ dv }{ dt } = \rho K - \mathrm{ grad } , p + \frac{ 1 }{ 3 } \eta , \mathrm{ grad } (\mathrm{ div } , v) + \eta \nabla ^ { 2 } v $$
電気が関わる現象については、この数式がある程度うまくいくことがわかっています。
\begin{align}
\mathrm{ div } , H = 0, \quad \mathrm{ rot } , E + \frac{ 1 }{ c } \frac{ \partial H }{ \partial t } = 0 \\\
\mathrm{ div } , E = \rho, \quad \mathrm{ rot } , H - \frac{ 1 }{ c } \frac{ \partial E }{ \partial t} = \frac{ 1 }{ c } \rho v
\end{align}
けれども、もし、あらゆる現象を寸分の狂いもなく、しかもたった一つの数式で説明することができたなら、それこそが創造主の設計図、つまり、神の数式と言えるのではないか。 物理学者はその数式を求める野望に、取り憑かれているのです。
すべての物理学者は、いわゆる万物の理論を見つけることを夢見ています。 自然界のありとあらゆるもの、素粒子の世界から大宇宙までを説明できる数式です。
ヨーロッパ合同原子核研究機構CERN フォビオラ・ジアノッティ
この世は何からできているのか。 神の数式を探し求めるための、血の滲むような道のり。 それは、いわば神の名に相応しい、完璧な美しい数式を求めようとする、苦難の連続でした。 大発見で打ち破った困難。 その一方で、完璧な美しさを追い求めるあまり、この世が、数式上は存在してはならないという、矛盾した結論に苦悩する年月も続きます。 そんな時、鉛筆のアイデアを引っさげて登場したのが、南部陽一郎。 完璧に垂直に立てた鉛筆でも、必ず倒れる運命にあるように、完璧な美しさは現実世界では、崩れる運命にあることを示し、神の数式への扉を開くことになるのです。
シリーズ、神の数式。 第1回は、この世界が何からできているのかを探る、第一線の物理学者の、100年に渡る、知られざる格闘の物語です。
第1回 この世は何からできているのか 〜天才たちの100年の苦闘〜
神の数式
これからお話するのは、物理学。 中でも、素粒子物理学と呼ばれる世界の人たちのお話です。 彼らは、この世のすべての出来事が、数式で書けるに違いないと、信じて疑わない、ちょっと変わった人たち。 頭の中は、とにかく、数式で、いつもいっぱいなんです。 そして、今日のお話のテーマは、宇宙の設計図。 つまり、神の数式を探し求める、天才物理学者たちの知られざる格闘のドラマを、垣間見ていただくことです。 私たちとは考え方がすっかり異なる物理学者たちは、どんな方法で、万物の理論に肉薄しようとしてきたのでしょうか。 実は、物理学者たちは、この100年間で神の数式にかなり近づいたというのです。 ヒッグス粒子を発見したCERNの裏庭に、一つの数式が刻まれていました。
皆さん、これこそが本日の主役、物理学者たちが神の数式に最も近いと考える、最先端の数式です。 「えー、さっぱりわけがわからない。」? いえいえ、大丈夫です。 この式を少し詳しく書くとこんな感じ。
\begin{align}
\mathscr{L} & = \bar{\psi}i\boldsymbol{\partial}\psi\\\
& \quad -g_{1}\bar{\psi}\mathbf{B}\psi-\frac{1}{4}\mathcal{B}^{\mu\nu}\mathcal{B}_{\mu\nu}\\\
& \quad -g_{2}\bar{\psi}\mathbf{W}\psi-\frac{1}{4}\mathcal{W}^{\mu\nu}\cdot\mathcal{W}_{\mu\nu}\\\
& \quad -g_{3}\bar{\psi}\mathbf{G}\psi-\frac{1}{4}\mathcal{G^{\mu\nu}}\cdot\mathcal{G}_{\mu\nu}\\\
& \quad +\bar{\psi}_{i}y_{ij}\psi_{j}\phi+h.c.\\\
& \quad +|D_{\mu}\phi|^{2}-V(\phi)
\end{align}
ちなみに1行目は、この世界を作り上げている物質の最小単位。 つまり、素粒子がどんな性質を持っているのかを表す、数式なのだと言います。 その素粒子はこの4種類。
- e 電子
- ν ニュートリノ
- u クォーク
- d クォーク
これらの素粒子がどこにあるのか、一応、見ておきましょう。 何しろ物質の最小単位ですから、小さな小さなミクロの世界に、それらは存在しています。 まず、原子の中をクルクル回っている電子。 ご存知の方も多いでしょ? そして、原子の中心の原子核を作り上げているのが、クォークと名付けられた2種類の素粒子です。 最後に、原子核から時折飛び出してくることがある、気まぐれな素粒子が、ニュートリノです。 では、これらの素粒子を、原子の中にまとめたり動かしたりしているものの正体は、一体なんでしょうか。 それを表しているのが、この3行です。
\begin{align}
& -g_{1}\bar{\psi}\mathbf{B}\psi-\frac{1}{4}\mathcal{B}^{\mu\nu}\mathcal{B}_{\mu\nu} & \text{ 電磁気力 }\\\
& -g_{2}\bar{\psi}\mathbf{W}\psi-\frac{1}{4}\mathcal{W}^{\mu\nu}\cdot\mathcal{W}_{\mu\nu} & \text{ 弱い核力 }\\\
& -g_{3}\bar{\psi}\mathbf{G}\psi-\frac{1}{4}\mathcal{G^{\mu\nu}}\cdot\mathcal{G}_{\mu\nu} & \text{ 強い核力 }\\\
\end{align}
再び原子でご説明すると、電子を原子核に引き寄せているのが、電磁気力。 そして、2種類のクォークをまとめ、原子核を作り上げているのが、強い核力、と呼ばれる力。 ニュートリノを原子核から飛び出させていた原因は、弱い核力、と呼ばれる力です。 物理学者たちは、先ほどの4つの素粒子と、この3つの力が完全に理解できれば、オーロラや台風だけでなく、この世のすべてが説明できると、信じているのです。 そして、最後の2行は、ヒッグス粒子の存在を示した部分。
\begin{align}
& +\bar{\psi}_{i}y_{ij}\psi_{j}\phi+h.c. & \text{ ヒッグス粒子 }\\\
& +|D_{\mu}\phi|^{2}-V(\phi) &
\end{align}
ヒッグス粒子がどんな役割を担っているのかは、後ほど詳しくご説明しますので、少しお待ちください。 物理学者は、この神の数式に最も近い数式に、どうやって辿り着いたのか、今から、その100年にわたる苦闘を、たどっていきましょう。 まずは1行目。
$$ \mathscr{L} = \bar{\psi}i\boldsymbol{\partial}\psi $$
物質の最小単位である素粒子を説明する、数式。 そこには、数式の美しさにとことんこだわった、一人の男の物語がありました。
ディラック方程式
神の数式探しの最初の舞台となったのは、1920年代後半の、ここ、ケンブリッジでした。 ここに、一人の若き物理学者が暮らしていました。 ポール・ディラック。 ケンブリッジ大学の中でも、最も権威のある、ルーカス教授職に、30歳の若さで就くことになる、天才です。 ちなみにこのルーカス教授職に就いた人物には、あのニュートンや、車椅子の天才、ホーキング博士がいるんです。 万物を説明する数式を探したい。 ディラックの興味は、まず、4種類の素粒子の内で、唯一発見されていた、電子に向かいました。 すでに電子は、マイナスの電気を持っていることはわかっていました。 さらにその性質を表す数式も知られていました。 シュレディンガー方程式。
$$ i\frac{\partial}{\partial t}\psi=-\frac{1}{2m}\sum\frac{\partial^{2}}{\partial x^{2}}\psi $$
この数式を使えば、電子のエネルギーなどを、ほぼ正しく求めることが可能でした。 ところが、その電子に、シュレディンガー方程式では、説明のつかない性質があることが、わかってきます。 いわば地球のように自転をし、さらに、磁石のような性質を持っているという事実でした。 なぜ自然は、自転する磁石のような、不思議な性質を電子に与えたのか。 ディラックはその性質を説明できる、新しい数式を作り出したいと考えたのです。 当時の物理学者の姿はこんな風に例えられます。 このとき持っていた最高の知識を武器に、素粒子の正しい数式を求めようとしたものの、まるで歯が立たなかったのです。 新しい数式を作ろうというディラックのアプローチは、非常に変わっていました。 それまでは、実験や観測結果を、そのまま数式に置き換えれば良いと考えられていました。 一方ディラックは自分の美的感覚に従うことにしたのです。 ディラックの座右の名。
物理法則は 数学的に美しくなければならない
ポール・ディラック
「え?美しさ?科学者にしてはずいぶん曖昧だなあ。」 とお思いになるかもしれません。 だって、人によってはこんな風景を美しいと感じるでしょうし。

また、ある人は、これを美しいと感じるでしょう。

美の感覚には、個人差がありますよね。 けれども、物理学者にとっての美しさは、対称性 と呼ばれ、その基準は、非常にはっきりしているのです。 設計図を描く製図台を使って、物理学者の見ている美しさを、ご説明しましょう。 例えば、この2つの図形。

物理学者なら、迷わず右を、美しいと考えます。 「まんまるなんだから当たり前だ。」? まあまあ、慌てずに。 物理学者は、こんな、xとyの座標軸 を使って、美を見極めているのです。
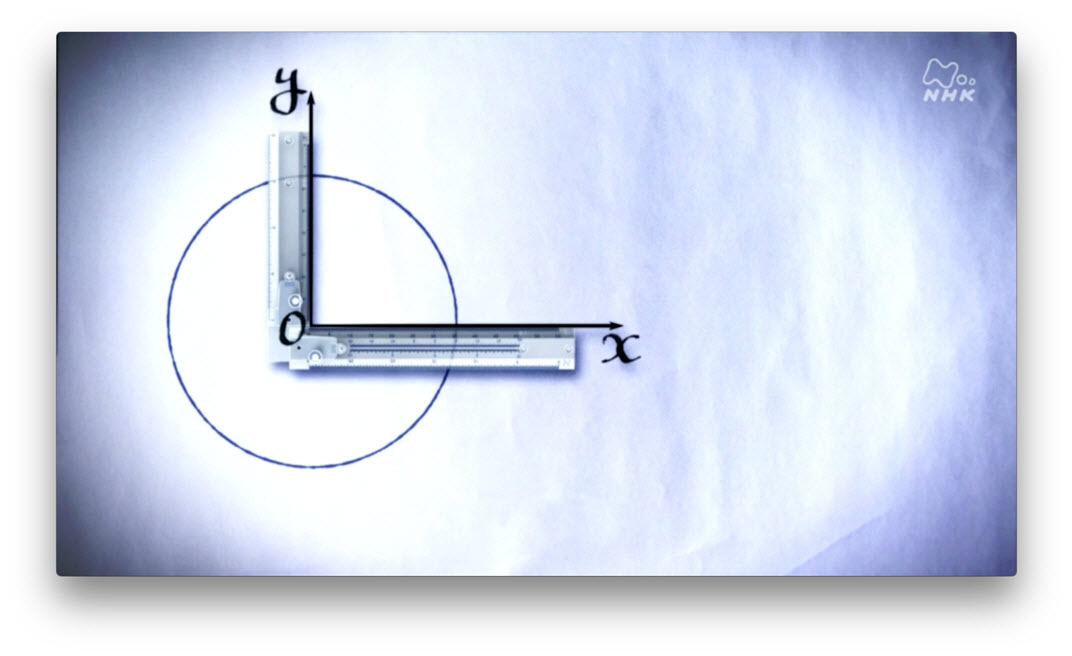
座標軸を通して、円の数式を見てみましょう。
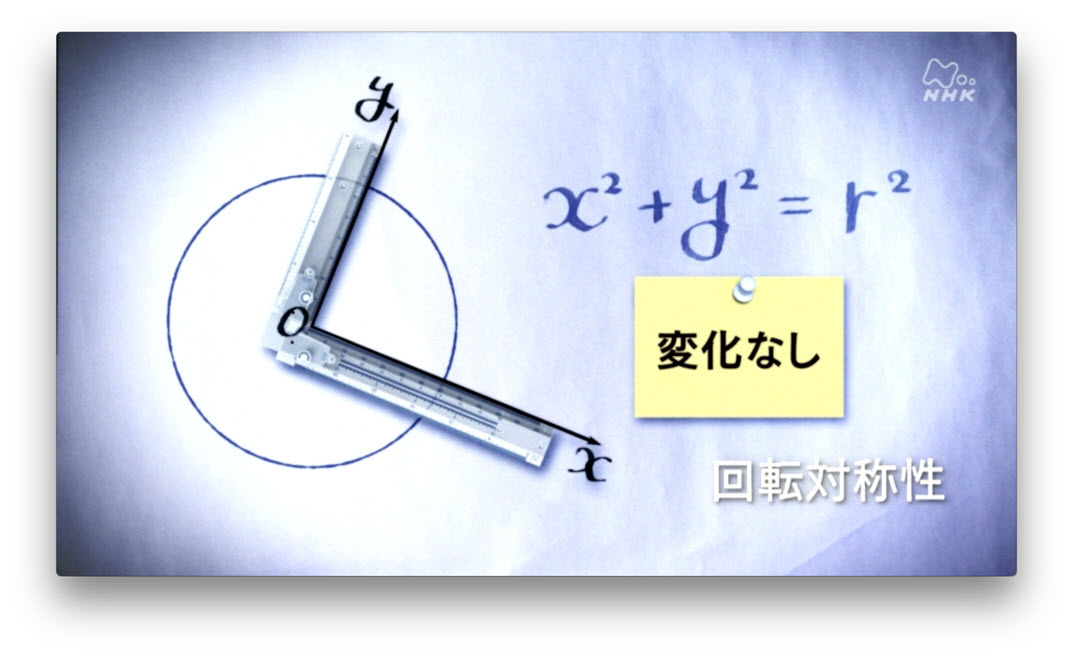
座標軸をこんな風に回転させたとしても、数式の形は変化しません。 このことが、すごいことだというのです。 この数式には、回転対称性 があるといい、物理学者は、これを美しいと感じるのです。 さらに物理学者は、こんな縞模様も大好きなんです。

それは、この模様を表す数式が、座標軸を平行にずらしてみたとしても、やっぱり変化しないからなのです。 こんな時、物理学者は、並進対称性 という美しさがあるといいます。 基準になる座標軸、つまり見る人の視点を変えても、数式が変わらないことが美しいのです。 ちなみに先ほどの円の数式は、座標軸が平行に移動すると、形がこんな風に大きく変化してしまいます。
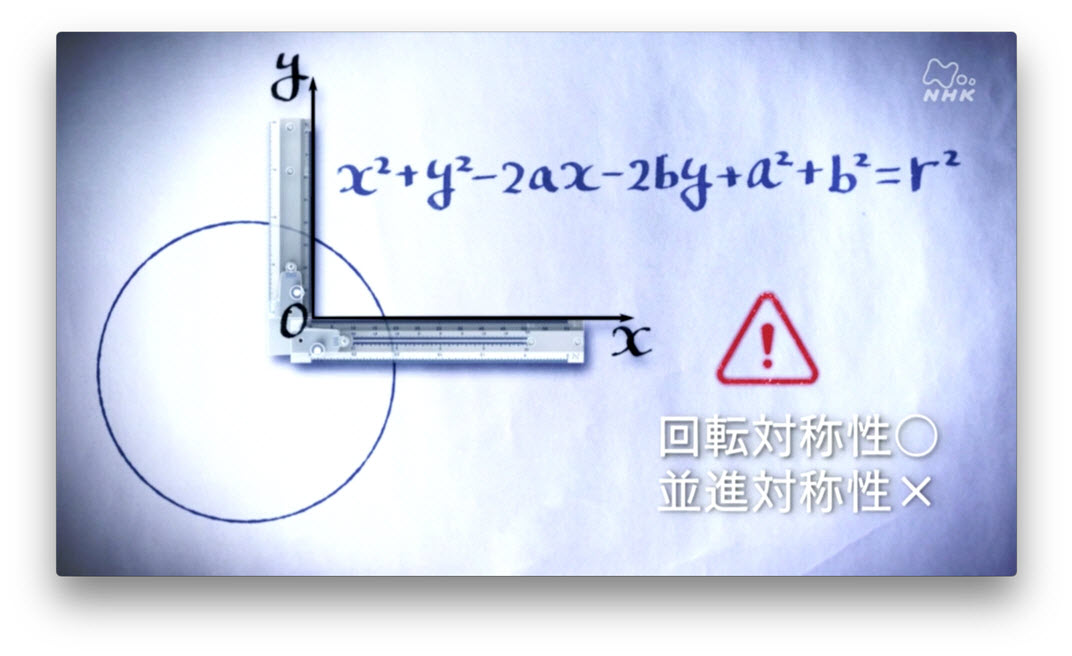
だから、円の数式は、回転対称性 は持っていますが、並進対称性 は持っていません。
対称性とは、見る人の視点が変わっても、元々の形や性質が、変わらないということです。 正方形は視点を90°回転しても、全く同じに見えますよね。 物理の数式も、見ている人の視点が変わったとしても、変化しないのです。
1979年 ノーベル物理学賞 スティーブン・ワインバーグ
さて、ディラックが大切にしていたもう一つの美しさがあります。 それは、ローレンツ対称性。 アインシュタインの相対性理論と関係があり、いわば、時間と空間は、本質的には同じものだという意味なのです。 その上で、ディラックはこんな風に考えました。 もし神が作った宇宙の設計図があるとするならば、それは完璧な美しさ、つまり、すべての対称性を持ったものにちがいない。 ここで試しに、あのシュレディンガー方程式を、見てみましょう。
$$ i\frac{\partial}{\partial \color{red}{t}}\psi=-\frac{1}{2m}\sum\frac{\partial^{2}}{\partial \color{red}{x^{2}}}\psi $$
よく見るとわかるように、時間を表す$t$が一つ、空間を表す$x$は2つ含まれています。 だから、時間と空間は同じものだという、ローレンツ対称性は、持っていなかったのです。 そのため、視点が変わると数式は、形が大きく崩れてしまうのです。

見る立場かかわると変化してしまう数式は、神の数式として相応しくない。 ディラックは、すべての対称性を持った、美しい数式の構築を、目指しました。 3か月間、書斎にこもりっきりになったディラック。 外部との接触を一切断ち切ります。 有頂天な気持ちと恐怖が、交互に現れ、何度もパニックに陥る日々。 しかし、美しさにとことんこだわった苦労は、報われます。 1928年に発表された論文です。
電子の量子論(ディラック 1928年)
そこに登場したのは、ディラック方程式。
$$ i\gamma\frac{\partial}{\partial \color{red}{t}}\psi+i\sum\gamma\frac{\partial}{\partial \color{red}{x}}\psi=m\psi $$
- 回転対称性:○
- 並進対称性:○
- ローレンツ対称性:○
$t$と$x$が一つずつ。 あのローレンツ対称性をも満たす、シンプルな数式でした。 その威力は、驚くべきものでした。 電子の自転や、磁石といった、謎めいた性質を、すべて正確に説明することができたのです。
ディラック方程式は、実に美しいものです。 初めて見た時、私は涙がこぼれました。 多くの物理学者は、ディラック方程式を見ると涙を流します。 電子の複雑で奇妙な性質が、対称性のおかげで、一つの数式にヒューっとまとまっているのですから。
ニューヨーク市立大学教授 ミチオ カク
さらに、その後見つかったニュートリノやクォークなど、物質の最小単位である、すべての素粒子の性質が、ディラック方程式で説明できることまで、わかりました。 すべての対称性を兼ね備えることで、素粒子の性質を完璧に説明する数式が、解明されたのです。 物理学者が目指す、神の数式に相応しい、完璧な美の世界が、初めて姿を現したのです。
ディラック方程式は、対称性の重要さを教えてくれました。 これ以降多くの物理学者が、対称性に真剣に目を向けるようになったのです。
プリンストン高等研究所名誉教授 フリーマン・ダイソン
物理学者たちが、神の数式を刻み込んだ石碑の1行目。 そこには、ディラック方程式が、コンパクトにまとめられ、刻み込まれました。
$$ \mathscr{L}=\bar{\psi}i\boldsymbol{\partial}\psi-\bar{\psi}M\psi $$
電磁気力の数式
この世は何からできているのか。 それを1つの数式で解き明かそうとする、物理学者たちの戦い。 次に立ちはだかったのは、素粒子どうしを結びつけたり動かしたりしている、3つの力の数式が、まだわかっていないという問題でした。 最初のターゲットは、3つの力の中で最も身近な、電磁気力 でした。 電磁気力は、原子核に電子を引き寄せ、さらには、原子どうしをまとめ上げ、様々な物質を生み出す源となっている力です。 1930年代、アメリカ西海岸に電磁気力の数式に挑む、一人の物理学者がいました。 ロバート・オッペンハイマー。 そうです。 その後、原爆の父、と呼ばれるようになる人物です。 あらゆる研究分野で、その名が轟いていました。
オッペンハイマーは、本物の天才でした。 彼は、物理学のあらゆる分野に通じ、物理学における理解を統合する、驚くべき力を持っていました。
ブランダイス大学 名誉教授 シルバン・シュウェーバ
オッペンハイマーたち、当時の物理学者の考え方は、こんな風に例えられます。 かつてディラックは、ローレンツ対称性という、美しさを武器に付け加えることで、素粒子の性質を表す数式に、導かれました。 同じように、何か新たな美しさ、つまり対称性を取り込めば、電磁気力を表す数式に、辿り着けるのではないかと、考えたのです。 オッペンハイマーたちが目をつけたのは、ゲージ対称性 と呼ばれる、4つ目の対称性でした。 ゲージ対称性は、難しい概念です。 けれど、ごく簡単に言えば、回転対称性に似ているのだとか。 電磁気の大きさを測る、こんな分度器が空間にあって、その角度を変えたとしても、数式の形は変化しない。 という美しさを、意味しているのだそうです。

ま、難しいことはともかく、物理学者たちは、ゲージ対称性を含む、4つの美しさを持った数式の構築を、模索しました。 すると、再び、1つの数式が、姿を現したのです。
\begin{align}
\mathscr{L} & = \bar{\psi}i\boldsymbol{\partial}\psi-\bar{\psi}M\psi\\\
& \quad -g\bar{\psi}\mathbf{A}\psi-\frac{1}{4}F^{\mu\nu}F_{\mu\nu}
\end{align}
- 回転対称性:○
- 並進対称性:○
- ローレンツ対称性:○
- ゲージ対称性:○
いわば、ディラック方程式の発展版。 4つの対称性を合わせもった、電磁気力の性質を説明する数式の、誕生でした。 数式から導き出された世界は、興味深いものでした。 電子は光子と呼ばれる光の粒を放ち、それが、電子と原子核を結びつけている。 電磁気力を伝える実体もまた、粒のような存在だというのです。 新たな対称性から導かれた電磁気力の数式は、この世の成り立ちを、見事に説明するだろう。 ところが、意外な事実が待っていたのです。
いろいろな計算を行ってみると、無限大という、全く意味がわからない数値が出てきたのです。 皆、数式が間違っているかもしれないと考えました。
フロリダ大学教授 ピエール・ラモン
これは、オッペンハイマーが発表した論文です。
場と物質の相互作用の理論について(オッペンハイマー 1930年)
実際に数式を使ってみると、電子のエネルギーは、無限大という数値になってしまい、それは、あらゆる物質が存在してはならないということを、意味したのです。 なぜ、無限大という、わけのわからない数値ばかりが出てくるのか。 オッペンハイマーは、仲間の物理学者と手分けをして、計算を何度もやり直しましたが、無限大の問題は、全く解消できませんでした。 このころ、時代の歯車は、大きく狂い始めます。 1939年9月、ドイツがポーランドへ侵攻。 第2次世界大戦が始まりました。 さらに、アメリカの物理学者、フェルミが、ウランの核分裂連鎖反応に成功。 多くの物理学者たちが、原爆の開発へと、駆り立てられることになったのです。 アメリカが誇る天才、オッペンハイマーは、マンハッタン計画の責任者に、任命されました。 ニューメキシコ州のロスアラモスに集まる、物理学者たち。 神の数式へ近づくための研究は、無限大の問題を解消できないまま、姿を消したのです。
何十万人もの命を奪った原爆。 ジャーナリストたちは、オッペンハイマーに、原爆の父、という称号を与えました。 その後、電磁気力の研究の第一線に戻ることは、ありませんでした。 純粋な理論物理学の世界で生きる道は、なかったのか。 戦後、自戒の念に苦しめられたオッペンハイマーに、思わぬ場所から手紙が届いたのは、1948年のことでした。 差出人は朝永振一郎。 名前も知らない日本人の物理学者でした。 自分は、戦争中に無限大の問題を解決する方法を見つけていた。 しかし、それを欧米に発表する機会を奪われていた。 という内容でした。 自分が開発した原爆の被害国からの思わぬ知らせに、オッペンハイマーは心を揺さぶられます。
オッペンハイマーは、手紙を受け取るとすぐに、日本で行われていた研究の重要さを、認識しました。 そして、朝永へ返事を書き、彼の研究を、世界に知らしめるため、権威ある物理学会紙に向け、論文を書くように勧めたのです。
ブランダイス大学 名誉教授 シルバン・シュウェーバ
英語に翻訳された朝永の論文は、オッペンハイマーの手助けで、世界で最も権威のある、フィジカルレビュー紙に掲載されました。
量子場理論での無限大の反作用について(朝永 1948年)
特殊な計算方法を開発し、無限大の困難を打ち破った論文に、世界は度肝を抜かれます。 あるアメリカの物理学者は、こう語りました。
戦争の廃虚と、混乱の最中にある日本で、国際的に完全に孤立状態にありながら、朝永はどうにかして、理論物理研究集団を維持し、ある意味では、世界のどこよりも進んだ研究を行っていた。 我々には深淵からの声のように響いた。
あるアメリカの物理学者
ちょうど同じ頃、朝永と全く同等の理論を、アメリカの若き物理学者、ファインマンとシュウィンガーが発表。 戦後の自由な空気の中、無限大の問題は、一気に解決したのです。 朝永たちがまとめ上げた数式による計算結果は、実験事実と驚くべき一致を見せました。 例えば、電子が持つ磁石の強さもその一つです。 対称性の美だけから導かれた数式の計算結果は、こんな数値。
- 理論:2.0023193043…
- 実験:2.0023193043…
それは、実験で測定された磁石の強さと、小数点以下10桁まで、ピタリと一致することになったのです。
全く不思議なことです。 なぜなら私たちは、電磁気力の数式が、これほどまでに正しいとは想像していなかったからです。 しかし、その数式は、驚異的な正確さを示したのです。
プリンストン高等研究所名誉教授 フリーマン・ダイソン
対称性という美に従えば、正しい数式を構築できる。 ディラックから始まった信念は、電磁気力の数式をも解明しました。 物理学者たちが辿り着いた、神の数式の2行目。 驚異的に正確な数式が、歴史に刻まれることになりました。
\begin{align}
\mathscr{L} & = \bar{\psi}i\boldsymbol{\partial}\psi-\bar{\psi}M\psi & \text{ 基本素粒子 }\\\
& \quad -g\bar{\psi}\mathbf{A}\psi-\frac{1}{4}F^{\mu\nu}F_{\mu\nu} & \text{ 電磁気力 }
\end{align}
強い核力と弱い核力の数式
見事に解明された電磁気力の数式。 しかし、続く1950年代。 神の数式の構築を目指す物理学者たちは、思いもよらぬ事態に翻弄されることになります。 その悲劇の主役となったのは、中国出身の風雲児、チェンニン・ヤン でした。 みなさん覚えていますか? 物質を構成するご覧の素粒子を、まとめたり動かしたりしている、3つの力を。
- e 電子
- ν ニュートリノ
- u クォーク
- d クォーク
すでに電子を原子核に引き寄せる電磁気力の数式は、解明されました。 ヤンが挑んだのは、原子核を作るクォーク同士を結びつけている、強い核力。 そして、ニュートリノを原子核から飛び出させる、弱い核力でした。 ヤンが、こうした力の数式を目指す手がかりにしたのも、美しさ。 つまり、対称性をさらに追求すれば、新たな力の数式もまた、構築できるはずだと考えたのです。
その数式を導く、基本的な原理があるはずでした。 私は、電磁気力の数式を導いた、ゲージ対称性を発展させようと考えたのです。
1957年 ノーベル物理学賞 チェンニン・ヤン
ヤンは、原子核の中に、ゲージ対称性と似た美しさが存在しないか、調べ始めました。 そして辿り着いたのが、物理学者にとっても超難解だと言われる、非可換ゲージ対称性 と呼ばれるものだったのです。 1954年、ヤンが同僚のミルズと共に発表した研究論文。
荷電スピンの保存とゲージ不変性(ヤン 1954年)
新たなゲージ対称性を数式に持たせることで、素粒子の間の、新たな力の数式に辿り着いくことができたのです。
$$ \mathfrak{L}=-\frac{1}{4}\mathbf{f}_{\mu\nu}\cdot\mathbf{f}_{\mu\nu}-\bar{\psi}\gamma_{\mu}(\partial_{\mu}-i\epsilon\boldsymbol{\tau}\cdot\mathbf{b}_{\mu})\psi-m\bar{\psi}\psi. $$
ヤンの数式は、電磁気力をヒントにしたものですが、それよりもさらに美しく、素晴らしい対称性を持っていたのです。 それは電磁気力を超えて、次の領域へと踏み出した、まさに偉業だったと言えるでしょう。
プリンストン高等研究所名誉教授 フリーマン・ダイソン
ヤンの理論を推し進め、それを現在の物理学の言葉で書き表すと、こんな数式になることがわかっています。
\begin{align}
\mathscr{L} & = \bar{\psi}i\boldsymbol{\partial}\psi-\bar{\psi}M\psi & \text{ 基本素粒子 }\\\
& \quad -g_{1}\bar{\psi}\mathbf{B}\psi-\frac{1}{4}\mathcal{B}^{\mu\nu}\mathcal{B}_{\mu\nu} & \text{ 電磁気力 }\\\
& \quad -g_{2}\bar{\psi}\mathbf{W}\psi-\frac{1}{4}\mathcal{W}^{\mu\nu}\cdot\mathcal{W}_{\mu\nu} & \text{ 弱い核力 }\\\
& \quad -g_{3}\bar{\psi}\mathbf{G}\psi-\frac{1}{4}\mathcal{G^{\mu\nu}}\cdot\mathcal{G}_{\mu\nu} & \text{ 強い核力 }
\end{align}
これで、物理学者たちが神の数式に最も近いと考えるものが、ヒッグス粒子の部分を除き、全部揃いました。
ついに、この世のすべての力と素粒子を表す数式が見つかった。 多くの物理学者が、期待に胸を躍らせました。 ところが、そこには全く予想外の落とし穴が、あったのです。 それは、強い核力や弱い核力を伝える粒子の重さが、どう計算しても、すべてゼロになってしまうという矛盾でした。 重さがゼロなのは光子だけで、その他の粒子は、すべて重さを持つはずだったのです。
光子は、ずいぶん前から質量がゼロである事は知られていました。 一方、原子核の中で力を伝える粒子は、まだ発見されていませんでしたが、明らかだったのは、その粒子は非常に重いということでした。 軽ければ当時の実験でも、発見されていたはずだったのです。
1979年 ノーベル物理学賞 スティーブン・ワインバーグ
数式は素晴らしく美しい。 しかし力の粒子の重さが、ゼロになってしまうという点で、現実とかけ離れている。 完璧な美しさを追い求めて来た物理学者の眼の前に、重さゼロという、大きな矛盾が姿を現したのです。 その後、間も無く、ヤンの理論について議論しようという物理学者は、ほとんどいなくなりました。 ヤン自身も、理論の完成を諦めます。 さらに物理学者たちを驚かせる出来事が続きます。 対称性のより深い研究から、力を伝える粒子だけでなく、物質の最小単位である、すべての素粒子の重さまでもが、数式上は、ゼロになってしまうという、驚くべきことが指摘されます。 つまり、世の中のすべてに重さがないという、現実とは矛盾した結論が、数式から導き出される事態になったのです。 もし、本当にすべての素粒子に、重さがないとしたならば、大変なことが起きます。 計算上、原子からは電子が飛び出し、物質はすべてバラバラになってしまうのです。
すべての素粒子の重さがゼロだったとしたら、あらゆるものが飛び散ります。 すべてが光の速さで飛び出すのです。 安定なものはなくなり、人も犬も猫もすべての都市もなくなります。 あらゆるものが光の速さで動き、原子を構成するものがなくなってしまうからです。
ニューヨーク市立大学教授 ミチオ・カク
さてさて、なんだか大変なことになってしまいました。 対称性という美しさに導かれ、神の数式に近づいていたはずの物理学者たち。 そのすぐ足元には、重さの謎という、深い深い落とし穴が、あったのです。 すべての謎が解かれるまでには、ヒッグス粒子の発見を、待たねばなりませんでした。
自発的対称性の破れ
突然現れた重さの謎に、どう立ち向かえばいいのか。 1960年代、アメリカシカゴに、それまでとは全くタイプの異なる物理学者が登場します。 日本生まれの、南部陽一郎。 人々は南部を、こう形容しました。
南部には未来が見えている。
人々
この異質の天才が、美しさに導かれると、なぜか重さがゼロになる、という大きな矛盾を、解決することになります。 1960年代初め、南部が最も興味を持っていたのは、いわばこの現象でした。 そうです。 番組の冒頭でご紹介した、倒れてしまう、鉛筆の問題。 単に鉛筆が倒れるなんでもない現象だと思うかもしれません。 しかし、この現象が、重さの矛盾を解くヒントになると、南部は気付いたのです。 こう考えてみてください。 ここに、鉛筆を真っ直ぐに立てるという設計図があったとしましょう。 真っ直ぐに立てなさいというのですから、この設計図は、回転対称性を実現するように、描かれています。 そして、設計図通り、実際に鉛筆を立ててみると、どうなるか。 現実は、設計図通りの回転対称性を持った状態には、なりません。 設計図には対称性があるのに、実際に起きる現実には、回転対称性はない。 その後、ノーベル賞に輝く、自発的対称性の破れ と呼ばれる現象です。 南部は、この、自発的対称性の破れが、自然界の設計図でも起き得ると、閃いたのです。
南部陽一郎が初めて示したのは、自然界の設計図に対称性があったとしても、我々が観測する物理現象には、その対称性がなくても良いということです。 数学的に言えば、自然現象を記述する数式に、対称性があっても、その数式から導きだされる現実には、対称性がなくても良いのです。
1979年 ノーベル物理学賞 スティーブン・ワインバーグ
1961年に南部が発表した、強い核力に関する研究論文。
超電導の類推による素粒子の動的模型(南部 1961年)
この内容を現在の物理学の言葉で言えばこうなります。 これは、強い核力の性質を表す数式。 つまり、強い核力の設計図です。
$$ g_{3}\bar{\psi}\mathbf{G}\psi $$
少し詳しく書くとこんな感じ。
$$ g_{3}(\bar{\color{red}{\mathrm{u}}}\mathbf{G}\color{red}{\mathrm{u}}+\color{red}{\bar{\mathrm{d}}}\mathbf{G}\color{red}{\mathrm{d}}) $$
- u:クォーク
- d:クォーク
強い核力を感じるクォークの姿が見えています。 この設計図は、一種のゲージ対称性に沿うように描かれていて、その結果、クォークの重さはゼロでなければなりません。 しかし、回転対称性を持つ鉛筆の設計図から、回転対称性がない現実が生まれたように、クォークの重さはゼロだとする設計図から、クォークに重さがあるという現実が生まれてくることを、南部は見抜いたのです。
対称性の破れに すぐに気付いたわけではない
長い間考えたあげくの ひとつの解決策
後になって考えれば 当たり前の現象だと分かった
南部陽一郎
南部が解決したことをわかりやすくまとめると、こうなります。 完璧な美しさを追い求めてきた結果、重さゼロ、という矛盾にぶち当たった物理学者たち。 しかし、南部は完璧な美しさは崩れる運命にあることを、倒れる鉛筆を例に示し、その結果、この世界に重さが生まれてくることを、証明したのです。 倒れる鉛筆という身近な存在から生まれた、自発的対称性の破れ。 それは、誰もが予想しなかった、大発見だったのです。
ヒッグス粒子
さて、強い核力からクォークの重さが自動的に生まれることは、わかりました。 しかし、強い核力を感じない電子やニュートリノ。 そして、弱い核力を伝える粒子などの重さが、数式上は、どうしてもゼロになるという問題が残っていました。 この問題に、ヒッグス粒子という、新手のアイデアで挑むことになるのが、スティーブン・ワインバーグでした。 ワインバーグはクォーク以外の素粒子にも重さを持たせるため、南部が提唱した、自発的対称性の破れを応用できないか、悩み続けていました。 そして、ついに、それまでの物理学者が決して踏み出さなかった、いわば、禁断の領域へと足を踏み入れます。 それは、この世には存在しない都合の良い粒子を、理論に持ち込むことでした。
私の理論では、ある種の新しい場というか、力というか、そういうものを持ち込みました。 それがどんな時でも、何もない真空をびっしりと埋めつくし、しかもそれが、宇宙全体に広がっているという考えです。 これが自発的に対称性を破るのです。
1979年 ノーベル物理学賞 スティーブン・ワインバーグ
当時ワインバーグが参考にした研究論文。
ゲージ粒子の質量と対称性の破れ(ヒッグス 1964年)
それによると、ある都合の良い素粒子、ヒッグス粒子を理論に持ち込めば、数式の美しい対称性は保ったまま、素粒子に重さを持たせることができると書かれていました。 その都合の良い粒子は、最初は空間にほとんど存在しないのにもかかわらず、その後、勝手に空間を埋め尽くすような粒子だと言います。 これは、最初は完璧な美しさを保っていた世界が、その後、勝手にその美しさを失うという、あの南部の考え方を応用したものでした。 さて、ワインバーグによると、このヒッグス粒子に邪魔されることで、電子などは行く手を阻まれ、動きにくくなります。 その動きにくさこそが、重さの正体だというのです。 1967年に登場した、ワインバーグの論文。
軽粒子の一つの模型(ワインバーグ 1967年)
ワインバーグは、ヒッグス粒子のアイデアで、電子や弱い核力の粒子にも、重さを与えることに、見事に成功しました。 重さの謎に翻弄されてきた物理学者たちは、ヒッグス粒子の力を借りて、ついに神の数式に辿り着いく道を見つけたのです。 ところが、当時ワインバーグの理論の評判は、決して良いものではありませんでした。 ヒッグス粒子が、あまりに都合が良過ぎるという違和感を、一部の物理学者が、拭いされなかったのです。
それは、美しくありませんでした。 本当に美しいものは、一目見て、これしかないと感じさせます。 何かを少しでも変えると、たちまち崩れてしまう。 ヒッグス粒子には、美しさはありませんでした。
1957年 ノーベル物理学賞 チェンニン・ヤン
.
私は、ヒッグス粒子をトイレのようだと思いました。 綺麗な家を成り立たせるためには、汚れ役が必要です。 ヒッグスはトイレのようでした。
1979年 ノーベル物理学賞 シェルドン・グラショウ
あの車椅子の天才、ホーキング博士は、なんと、ヒッグス粒子は存在しない方に金銭まで賭けたのです。 そして迎えた2010年。 ワインバーグの理論の発表から、40年以上の年月が流れていました。 ヒッグス粒子を見つけるため、人類史上最大のエネルギーを、空間の一点に注ぎ込む実験装置が、ついに動き始めました。 2年以上にわたる実験を経て、ヒッグス粒子が叩き出されたと思われるシグナルが、捉えられたのです。
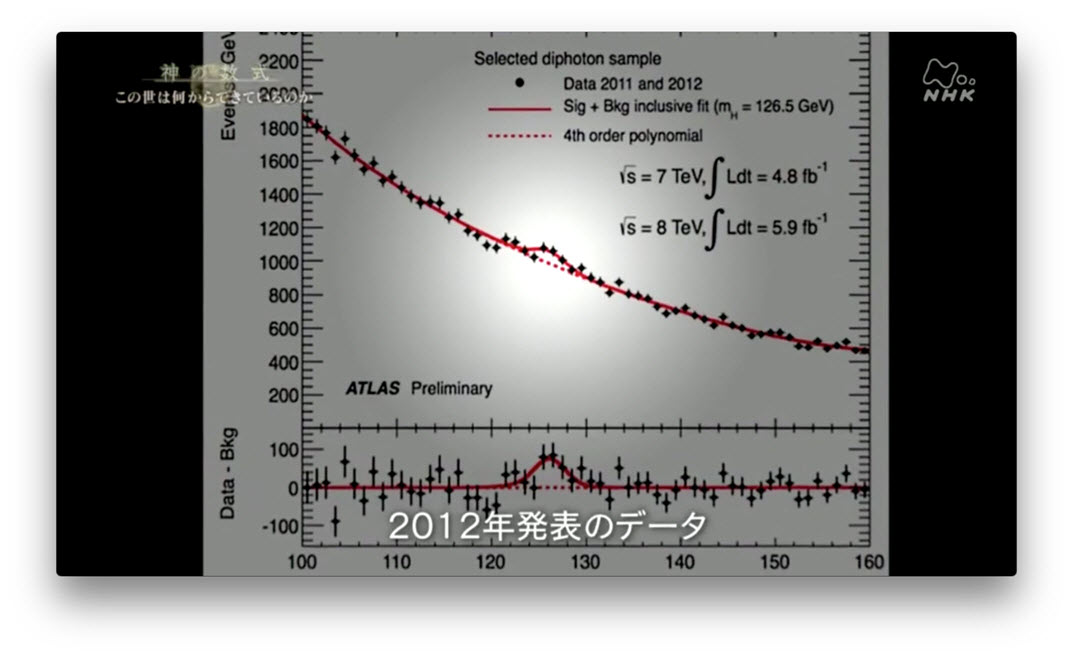
私たちはついに 新しい素粒子を発見しました
ヒッグス粒子だと思います
ヨーロッパ合同原子核研究機構CERN
ワインバーグの理論が実証されたと、世界中が讃えました。 物理学者たちが辿り着いた一つの数式。
\begin{align}
\mathscr{L} & = \bar{\psi}i\boldsymbol{\partial}\psi & \text{ 基本素粒子 }\\\
& \quad -g_{1}\bar{\psi}\mathbf{B}\psi-\frac{1}{4}\mathcal{B}^{\mu\nu}\mathcal{B}_{\mu\nu} & \text{ 電磁気力 }\\\
& \quad -g_{2}\bar{\psi}\mathbf{W}\psi-\frac{1}{4}\mathcal{W}^{\mu\nu}\cdot\mathcal{W}_{\mu\nu} & \text{ 弱い核力 }\\\
& \quad -g_{3}\bar{\psi}\mathbf{G}\psi-\frac{1}{4}\mathcal{G^{\mu\nu}}\cdot\mathcal{G}_{\mu\nu} & \text{ 強い核力 }\\\
& \quad +\bar{\psi}_{i}y_{ij}\psi_{j}\phi+h.c. & \text{ ヒッグス粒子 }\\\
& \quad +|D_{\mu}\phi|^{2}-V(\phi)
\end{align}
この世界を作る4種類の素粒子と、3つの力を、矛盾なく書き表した 標準理論 が、完成したのです。 ヒッグス粒子を発見したCERNの片隅には、神の数式に最も近いとされるその数式が刻まれました。
それは、物理学者たちの、100年にわたる戦いの金字塔だったのです。
Epilogue
神の数式の美しい対称性が、この世界にどのように反映されているのか。 今、物理学者たちは、ビッグバン以来の宇宙の歴史の中で、次のように解釈しています。 宇宙は、設計図である神の数式に従って誕生し、当初は、設計図通りの完璧な対称性を保っていた。 そこでは、あらゆる素粒子に重さがなく、バラバラに飛び回っていた。 しかし、ヒッグス粒子などが引き起こす、自発的対称性の破れによって、素粒子に重さが生まれた。 その結果、素粒子がまとまり、原子が作られ、星々が輝き始め、銀河も形成されていった。 今、私たちの暮らしが存在することも、いわば、神の数式に織り込まれていたのだというのです。 ヒッグス粒子の発見によって、標準理論は、今や、この世界に説明できない現象はないとまで言われるようになっています。 しかし、標準理論を構築した物理学者たちは、理論の完成を喜ぶよりも、むしろ、今、その先を目指し始めています。 標準理論の完成のためにヒッグス粒子の導入に踏み切った、スティーブン・ワインバーグ。 万有引力、つまり、重力を取り込んだ理論の構築が必要だと考えています。 素粒子の世界では、素粒子があまりに軽いため、それまで考えに入れる必要がなかった重力。 今、物理学の最先端では、この重力をも取り入れなければ、本物の神の数式には辿り着けないという考え方が、支配的になっています。
私たちは、単に3つの力の、数学的に美しい理論だけでは満足しません。 そこには重力が入っていないからです。 物理学の数式によって、あらゆる自然現象が説明できるはずだ。 という考え方は20世紀に始まった新しい思想でした。 それは大きな哲学的変革をもたらしました。 我々は今もなお、その知の変革を求めて続けているのです。
1979年 ノーベル物理学賞 スティーブン・ワインバーグ
およそ100年の歳月をかけて、この世の成り立ちを解明してきた物理学者たち。 神の数式を探し求める戦いは、今もまだ、終わっていません。