PYTHON BAYESIAN OPTIMIZATION でバックテストのパラメーターを最適化してみました

Bayesian Optimization を使ってみたかったので、これを使ってバックテストのパラメーターを最適化してみました。

環境

Python 3.6.5
Bayesian Optimization 1.0.0

Bayesian Optimization

「Bayesian Optimization」で検索して、ベイズ最適化についてざっくり理解しました。

後で知ることになりますが、自分の理解がざっくりすぎて問題に対して意味のある解決になっていないようでした…。

具体的なパッケージは Python の次のものを使いました。

GitHub - fmfn/BayesianOptimization: A Python implementation of global optimization with gaussian processes.

バックテストの関数

次のようなバックテストの関数を作りました。

def test(df, periods1=5, periods2=20, pip=0.01, spread=0.3, unit=10000):
    sp = pip * spread * unit
    bs = pd.Series(np.full(df.index.size, np.nan), index=df.index)
    pl = pd.Series(np.full(df.index.size, np.nan), index=df.index)
    entry = ls = np.nan
    ma1 = df['close'].rolling(periods1).mean()
    ma2 = df['close'].rolling(periods2).mean()
    df2 = pd.concat([df, ma1.shift(1), ma2.shift(1)], axis=1)
    for row in df2.itertuples():
        time, open_, high, low, close, ma1, ma2 = row
        if np.isnan([ma1, ma2]).any():
            continue
        if ma2 < ma1:
            if ls < 0:
                # exit (short position)
                pl[time] = (open_ - entry) * unit * ls - sp
            if not 0 < ls:
                # entry (long position)
                bs[time] = ls = 1
                entry = open_
        if ma1 < ma2:
            if 0 < ls:
                # exit (long position)
                pl[time] = (open_ - entry) * unit * ls - sp
            if not ls < 0:
                # entry (short position)
                bs[time] = ls = -1
                entry = open_
    if not np.isnan(ls):
        pl[time] = (close - entry) * unit * ls - sp
    return bs, pl

移動平均クロスオーバートレーディング戦略です。

パラメーターの初期値は 5 (periods1) と 20 (periods2) にしてみました。これを米ドル／円の日足の 2003/5/5~2018/1/2 までの期間で実行してみました。（ヒストリカルデータはこの記事のものです）

損益のグラフです。

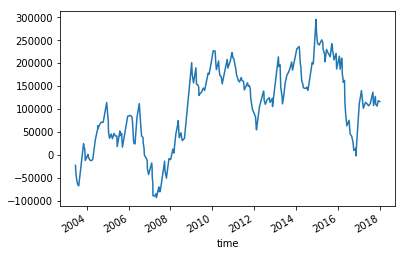
適当に設定した移動平均線のパラメーター（5 と 20）で、最終的に 10 万円くらいの利益にはなっているようです。

最適化

最初に、総損益が最大化することを目的とした関数を作りました。

def f(x, y):
    x2 = int(x)
    y2 = int(y)
    if y2 <= x2:
        return 0
    bs, pl = test(df, periods1=x2, periods2=y2)
    return pl.dropna().sum()

パラメーターを受け取って、バックテストして、そのときの総損益を返しているだけです。

次に、 BayesianOptimization のパッケージを使うための設定をしました。

from bayes_opt import BayesianOptimization

# Bounded region of parameter space
pbounds = { 'x': (1, 200), 'y': (1, 200) }

optimizer = BayesianOptimization(
    f=f, # 最大化したい関数
    pbounds=pbounds, # パラメーターの範囲
)

パラメーターの範囲は短期の移動平均線（x）も長期の移動平均線（y）も 1~200 にしてみました。

最適化をしました。

%%time
optimizer.maximize(
    init_points=5, # 初期観測点の数
    n_iter=25, # 何点評価するか
)

Jupyter Notebook で実行していると経過を表示してくれます。次のような経過になっていました。

|   iter    |  target   |     x     |     y     |
-------------------------------------------------
|  1        | -1.86e+05 |  151.4    |  168.6    |
|  2        |  6.431e+0 |  41.85    |  125.1    |
|  3        |  0.0      |  98.6     |  54.17    |
|  4        |  0.0      |  165.9    |  38.08    |
|  5        |  5.541e+0 |  5.764    |  133.4    |
|  6        |  6.431e+0 |  41.85    |  125.1    |
|  7        |  6.431e+0 |  41.84    |  125.1    |
|  8        |  6.431e+0 |  41.84    |  125.1    |
|  9        |  6.431e+0 |  41.84    |  125.1    |
|  10       |  6.431e+0 |  41.84    |  125.1    |
|  11       |  6.431e+0 |  41.84    |  125.1    |
|  12       |  6.431e+0 |  41.84    |  125.1    |
|  13       |  6.431e+0 |  41.84    |  125.1    |
|  14       |  6.431e+0 |  41.84    |  125.1    |
|  15       |  6.431e+0 |  41.84    |  125.1    |
|  16       |  6.431e+0 |  41.84    |  125.1    |
|  17       |  6.431e+0 |  41.84    |  125.1    |
|  18       |  6.431e+0 |  41.84    |  125.1    |
|  19       |  6.431e+0 |  41.84    |  125.1    |
|  20       |  6.431e+0 |  41.84    |  125.1    |
|  21       |  6.431e+0 |  41.84    |  125.1    |
|  22       |  6.431e+0 |  41.84    |  125.1    |
|  23       |  6.431e+0 |  41.84    |  125.1    |
|  24       |  6.431e+0 |  41.84    |  125.1    |
|  25       |  6.431e+0 |  41.84    |  125.1    |
|  26       |  6.431e+0 |  41.84    |  125.1    |
|  27       |  6.431e+0 |  41.84    |  125.1    |
|  28       |  6.431e+0 |  41.84    |  125.1    |
|  29       |  6.431e+0 |  41.84    |  125.1    |
|  30       |  6.431e+0 |  41.84    |  125.1    |
=================================================

総損益は指数の表現になっていて見づらいですけれども。

次のプロパティに最大値の結果が入っています。

optimizer.max

結果です。

{'target': 643099.9999999998,
 'params': {'x': 41.845420068232286, 'y': 125.07039719675709}}

このパラメーターでバックテストしたときの損益のグラフです。

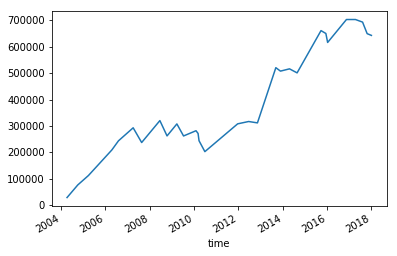
これはドローダウンが小さくてかなり良いところの結果が得られたようでした。何度か最適化をしてみましたけれども、結果に大きな差があるように感じました。総損益が 60 万円を超えることもあれば、 5 万円程度のときもありました。

上にあるような BayesianOptimization が出力してくれる経過を見ていると、初期観測点の数である 5 つの観測点をもとに 6 点目を評価したときに、もう結果が決まってきてしまう感じでした。だから 7 点目の評価以降はほとんどパラメーターが変わっていません（小数点以下だけが変わっているようでした）。毎回こんな感じでした。初期観測点の数が少なすぎるのかな？ベイズ最適化に関するカーネルとか獲得関数とか、最初に挙げたリンクの記事の内容を深く理解していないのですけれども、それを調整したら改善されるものなのかな？

参考程度に、 x が 1~200 、 y が 1~200 の組み合わせをすべて実行してみました。バックテストを 4 万回しました（半分は短期の移動平均線≧長期の移動平均線になってしまうので実際には実行していませんけれども）。 30 分くらいかかりました（電源につないでいなくてバッテリーだったので通常より遅かったかもしれません）。

Matplotlib のサンプルを参考に、その結果をグラフにしてみました。

濃い緑が総損益が高くなるところです。これによると、短期の移動平均線（x）が 25~75 の範囲、長期の移動平均線（y）が 50~125 の範囲あたりが良さそうなパラメーターになりそうです。

Matplotlib に 3D のサンプルもあったので 3D にしてみました。

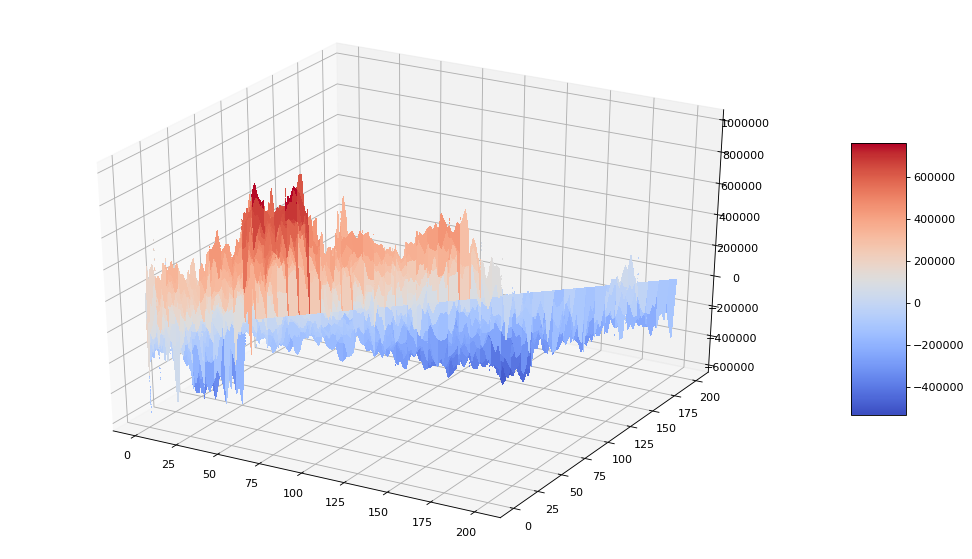
ちょっと 3D は見づらかったかもしれません。

でも、この 3D の山とか谷がガウス過程に従う前提があるからベイズ最適化を使うことができるんですよね（合ってるかな？）。

ガウス過程に従う関数fのn点はn次元ガウス分布に従う

ベイズ的最適化(Bayesian Optimization)の入門とその応用

そうだとすると、ガウス過程に従う保証がないならベイズ最適化は使っちゃいけないのかな？機械学習のハイパーパラメーターサーチってそういう保証があるものなのかな？

理解が浅くて意味のあることをした気がしません…。

応用数学

ここからは調べている途中で知ったことを書いておきます。

BayesianOptimization のパッケージから受け取るパラメーターを int にしたかったので調べていました。そして次の内容を見つけました。

2. Dealing with discrete parameters

There is no principled way of dealing with discrete parameters using this package.

Ok, now that we got that out of the way, how do you do it? You're bound to be in a situation where some of your function's parameters may only take on discrete values. Unfortunately, the nature of bayesian optimization with gaussian processes doesn't allow for an easy/intuitive way of dealing with discrete parameters - but that doesn't mean it is impossible. The example below showcases a simple, yet reasonably adequate, way to dealing with discrete parameters.
def func_with_discrete_params(x, y, d):
    # Simulate necessity of having d being discrete.
    assert type(d) == int
    
    return ((x + y + d) // (1 + d)) / (1 + (x + y) ** 2)

def function_to_be_optimized(x, y, w):
    d = int(w)
    return func_with_discrete_params(x, y, d)

optimizer = BayesianOptimization(
    f=function_to_be_optimized,
    pbounds={'x': (-10, 10), 'y': (-10, 10), 'w': (0, 5)},
    verbose=2,
    random_state=1,
)
BayesianOptimization/advanced-tour.ipynb at master · fmfn/BayesianOptimization · GitHub

最初は安易に BayesianOptimization のパッケージから int を渡す方法はないから、 int に変換する処理を実装する必要があるんだ、程度に認識しました。

そして最適化のことも調べてみたら、最適化は二つに分類できることを知りました。

最適化問題

数理最適化 - 最適化問題のうち、解が連続的なもの。数学において、ある条件に関して最もよい元を利用可能な集合から選択すること。

組合せ最適化 - 最適化問題のうち、解が離散的なもの。

最適化 - Wikipedia

BayesianOptimization はどちらかというと「数理最適化」に適用できるもののようでした（だからあえて離散的なパラメーターについての説明があるんだと解釈しました）。そして、今回やろうとしているバックテストのパラメーターの最適化は「組合せ最適化」に該当するようでした。これらを踏まえるとバックテストのパラメーターの最適化に BayesianOptimization はあまり適さないように感じましたけれども？

でも、ベイズ最適化を使って機械学習のハイパーパラメーターサーチをしているような記事をいくつか見かけました。

最も基本的な例である機械学習のハイパーパラメーターサーチにおいてはマニュアルであったり、自動的にやるとしたらgrid searchやrandomでやるということが多いかと思います。しかしベイズ最適化を使えばもっと上手く行うことができます。

ベイズ最適化入門 - Qiita

でも、そういう記事の中でのベイズ最適化の説明は数理最適化について言っているように見えました。

ベイズ最適化の具体的な説明

上のgifが大体のベイズ最適化の説明になっています。

ベイズ最適化入門 - Qiita

機械学習のハイパーパラメーターサーチって、組合せ最適化のような印象を持ったのですが（あるいは最適化問題には該当しないから数理最適化でも組合せ最適化でもないとか？）、機械学習をしたことがないのでわかりません…。バックテストのパラメーターの最適化にベイズ最適化を使うのは一般的なのかな？あまりに知識がなさ過ぎて、こういう疑問を持っていることがおかしいのかどうかもわかりません…。

もう少し調べていると、こういうのは「応用数学」という言葉にまとめられるようでした。

応用数学の研究対象は非常に幅が広く様々な分野に跨るため、関わる分野全てを挙げることは困難である。ここでは応用数学と関わり合いが特に深い代表的な分野を挙げる

数値解析

…略…

組合せ論

最適化問題・オペレーションズ・リサーチ

…略…

機械学習

統計学

…略…

応用数学 - Wikipedia

数学の知識が必要そうでした。小学校の算数も十分に理解していないから、先は長そうです…。

終わり

BayesianOptimization をただ使うだけなら簡単だったけれども、堅牢なシステムを作る目的を達成するために一番良い方法が本当にそれだったのか？という観点から見ると、そうではなかったように感じます。

目的を達成する（問題を解決する）ために一番良い方法を選択するためには、選択可能なものについて深い理解が必要だと痛感しました。その前にまず何が選択可能なのか知る必要もありますし。

Jupyter Notebook のファイルを Gist にアップロードしておきました。

Python Bayesian Optimization でバックテストのパラメーターを最適化してみました

環境

Bayesian Optimization

バックテストの関数

最適化

応用数学

終わり