『禁断の市場』を読んで試してみたことの続きです。 前回はランダムウォークのグラフを確認しました。 そして正規分布のグラフができました。 今回は米ドル/円のヒストリカルデータをもとにグラフを作って比較してみます。
環境
- Ubuntu 18.04 LTS
- Python 3.6
- Jupyter Notebook 5.2.0
- NumPy 1.14.4
- pandas 0.23.0
- matplotlib 2.2.2
米ドル/円のヒストリカルデータ
データは以前作ったものを使いました。 デューカスコピーからダウンロードした 1 分足のヒストリカルデータを日足にしたものです。
$ head ~/Documents/data/d/USDJPY_D.csv
time,open,high,low,close,volume
2003-05-05,118.94,119.046,118.461,118.603,592866.9
2003-05-06,118.591,118.751,117.29,117.5,581707.0
2003-05-07,117.456,117.83,116.052,116.303,584496.2
2003-05-08,116.311,116.969,115.94,116.823,588236.7
2003-05-09,116.835,117.612,116.794,117.151,583132.9
2003-05-12,117.286,117.286,116.304,117.025,586660.3
2003-05-13,117.053,117.528,116.338,116.561,584984.4
2003-05-14,116.554,116.837,115.557,116.16,586464.9
2003-05-15,116.173,116.525,115.282,116.515,585585.1
比較
ここからは Jupyter Notebook のセルに入力しながら進めます。
最初に必要なモジュールを読み込みました。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
米ドル/円のヒストリカルデータを読み込みました。
dtype = { 'time': str, 'open': float, 'high': float, 'low': float, 'close': float, 'volume': float }
names = ['time', 'open', 'high', 'low', 'close', 'volume']
df = pd.read_csv('~/Documents/data/d/USDJPY_D.csv', dtype=dtype, header=0, index_col='time', names=names, parse_dates=['time'])
df.head()
終値だけ使いたいので、終値だけのデータを s11 にしました。
それから変位のデータを s12 にしました。
s11 = df['close']
s12 = (s11 - s11.shift(1)).dropna()
次にランダムなデータを作りました。
標準偏差に収まる範囲を米ドル/円と同じにしたかったので sigma を s12.std() にしています。
ランダムなデータも変位を用意して s22 にしました。
n = s11.index.size
mu = 0
sigma = s12.std()
openprice = s11.head(1).item()
s21 = pd.Series(sigma * np.random.randn(n) + mu, index=s11.index).cumsum() + openprice
s22 = (s21 - s21.shift(1)).dropna()
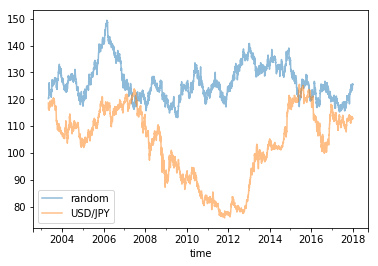
データを折れ線グラフで表示しました。
s21.plot(label='random', alpha=0.5)
s11.plot(label='USD/JPY', alpha=0.5)
plt.legend()
plt.show()
結果です。
変位の分布を表示しました。
density=True の引数を渡して標準偏差に収まる範囲のデータが 1 になるように正規化してみました。
これをつけないと思ったような比較のグラフになりませんでした。
n, bins, patches = plt.hist(s22, 100, label='random', alpha=0.5, density=True)
n, bins, patches = plt.hist(s12, 100, label='USD/JPY', alpha=0.5, density=True)
plt.legend()
plt.show()
結果です。
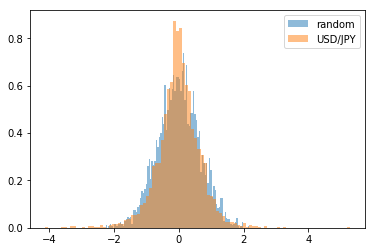
思った通りのグラフができました。
変位も折れ線グラフで表示してみました。
s22.plot(label='random', alpha=0.5)
s12.plot(label='USD/JPY', alpha=0.5)
plt.legend()
plt.show()
結果です。
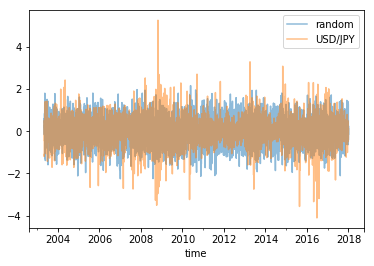
こちらも思った通りのグラフができました。
市場の特徴
作ったグラフからわかった市場の特徴を書いてみたいと思います。
変位の分布
中くらいの変動が期待するほどは多くはなく、非常に小さい変動と非常に大きな変動が目立つのです。
禁断の市場 第10章 ノア、ヨセフ、そして市場のバブル
変位の分布からは引用したような特徴がわかります。
非常に大きな変動は「ファット・テール」と名づけられていて、よく聞きます。 非常に小さい変動は名前もなくてあまり聞かないですけれども、正規分布よりも頻繁に起こるみたいです。 上で作った変位の分布は非常に大きな変動よりも非常に小さい変動の方が目立ちます(対数グラフにしていないからかもしれません)。
変位の折れ線グラフ
つまり、大きな突然の変動と平穏な状態が交互に繰り返される間欠的な性質と、その間隔がスケールに依存しないフラクタルになっているということです。
禁断の市場 第12章 禁断の金融10カ条
変位の折れ線グラフは他ではあまり見たことがなかったのですが、引用した特徴を表していると思いました。
上で作ったグラフは日足のヒストリカルデータで確認しましたけれども、 1 時間足のデータでも同じような特徴を確認しました。 参考までに 2005 年、 2010 年、 2015 年の 1 時間足のデータの変位の折れ線グラフです。
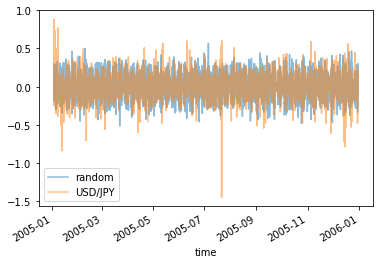
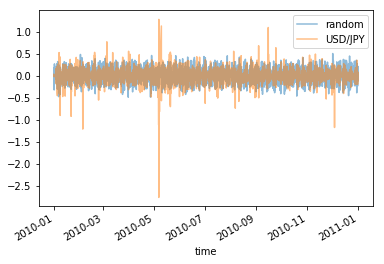
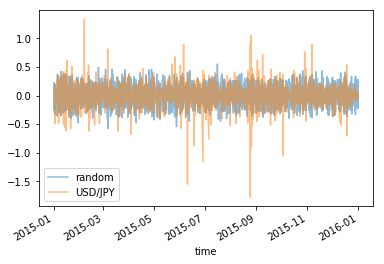
部分を切り取って拡大してみても同じような特徴がありました。
キーワードはマルチフラクタルです。 フラクタルの定義を思い出して下さい。 フラクタルは、全体を一定の割合で縮小すると部分が再現できます。 それに対し、マルチフラクタルは、一つの物のなかに複数の拡大縮小に関する特性を持っています。 場所や方向によって拡大縮小する比率が異なるのです。
禁断の市場 第11章 トレーディング時間のマルチフラクタル性
これがマルチフラクタルということみたいです。 いや、確認できたのはフラクタルということだけかなあ。 マルチフラクタルであることが確認できるのは、もっと時間と価格を複数確認してみてわかることかもしれません。
価格の変動は過去のデータに依存する場合があるのは確かですし、正規分布はまったく事実に反します。 数学的に言えば、市場は相関なしで依存性を示します。 ちょっと矛盾したような表現ですが、符号の付いた量である変位を見るか、負の値をとらない変位の大きさを見るかの違いです。 変位の符号は過去の値に無相関に決まるものとします。 昨日、価格が下落したとしても、今日の価格が下落するわけではありません。 それでも、価格の変位の大きさに過去との依存性を持たせることは可能です。 普段よりもはるかに大きな10%も価格が下落した翌日に10%上昇するということはありうることです。 しかし、翌日が10%の下落になる可能性も同じだけあり、上がるか下がるかの予測はできない、ということです。 変位の大きさには強い依存性があっても、価格の変位の相関は0になります。 大きな価格の変動は、直前の大きな変動の後に出てくる可能性が高くなります。 これは、ボラティリティ・クラスターと呼ばれる現象です。
禁断の市場 第12章 禁断の金融10カ条
上がるか下がるかは予測できない、けれども、ボラティリティは予測できるみたいです。
そうすると普通に為替の取引をしても利益は見込めないんじゃないかと思ってしまいます。 そしてオプションなら大きな利益が見込めるんじゃないかと思ってしまいます(オプションに詳しくないのですが、あれってボラティリティを取引している要素もあるんですよね?)。
終わり
比較してみて実際の市場について少し理解が深まったように思います。
わたしはボリンジャーバンドを使うことが多かったので、正規分布と比較して良かったです。 ボリンジャーバンドは正規分布や標準偏差を活用したインディケーターなので、チャートを見るときにこれらの比較がかなり影響してくるように思います。
中くらいの変動が期待するほどは多くはなく、非常に小さい変動と非常に大きな変動が目立つのです。
ボリンジャーバンドの正規分布と比較すると、中くらいの変動が期待するほど多くはないそうです。 だから非常に小さい変動を利益につなげること、非常に大きな変動を利益につなげること、これらを意識すると良さそうに思いました。
Gist に Jupyter Notebook をアップしておきました。