『禁断の市場』という本を読みました。 ランダムウォークのことが書かれていたので、 SciPy を使ってランダムウォークのグラフを作ってみました。
環境
- Ubuntu 18.04 LTS
- Python 3.6
- Jupyter Notebook 5.2.0
- NumPy 1.14.4
- pandas 0.23.0
- matplotlib 2.2.2
ランダムウォーク
17世紀のフランスではパスカルとフェルマー(彼の有名な「大定理」は証明されるのに350年もかかりました)がギャンブル好きの貴族のために確率論を発明しました。 そして、1900年にバシェリエは、ファンダメンタル分析とテクニカル分析のどちらともまったく違う視点に立ち、確率論に基づく定式化を行い、フランス国債の相場の問題に応用したのです。 ランダムウォークと呼ばれるこのモデルは、パスカルとフェルマーのモデルによく似ていました。 彼は、相場はコインの表・裏とまったく同様に等しい確率で上下すると考えました。 ラジオから聞こえてくるザーという雑音のように、市場価格の変化は無意味で特徴のないものだと想定したのです。 そして、上がり下がりの予測をするのではなく、変動の分布を考察しました。 もしも、市場価格がランダムウォークなら、68%の確率でデータは標準偏差の範囲内に入るはずです。 標準偏差の2倍に枠を広げれば、95%の変動をカバーすることができることになります。
禁断の市場 第1章 リスクとリターン
ランダムウォークの提唱者はバシェリエという人みたいです。 知らない人でした。
フェルマーは名前だけ聞いたことがあります。 彼の有名な「大定理」(フェルマーの最終定理 - Wikipedia)も内容は知らないですけれども、名前だけは聞いたことがあります。
コインの表・裏
ここから Jupyter Notebook のセルに入力しながら進めます。
必要なモジュールを読み込みました。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
コインの表・裏なので、表は 1 、裏は -1 になるようにしました。 ランダムに 1 と -1 が決まるようにしました。 サイズは 10000 にしました。
s = pd.Series(np.random.choice([1, -1], size=10000))
コインの表・裏のように決めたデータを積み上げて s2 にしました。
それを折れ線グラフで表示しました。
s2 = s.cumsum()
s2.plot()
結果です。
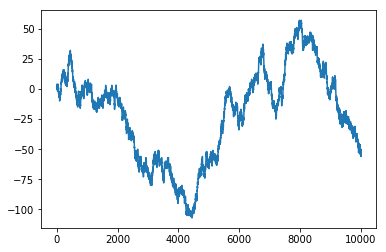
コインの表・裏のように決めたデータ s の分布を表示しました。
n, bins, patches = plt.hist(s, 100)
plt.show()
結果です。

1 か -1 のデータなので分布は両極端になりました。
ちょっとイメージしていたものと違いました。 正規分布のグラフを作りたかったのですけれども。
ランダムウォークの説明でよくある“コインの表・裏”という例えは“確率”だけのことを言っているみたいでした。 変動幅については言ってないように感じました。 たぶん。
彼は、相場はコインの表・裏とまったく同様に等しい確率で上下すると考えました。
上の引用でもこのコインの表・裏の例えのところには“確率”って書いてありました。
せっかくなので作ったデータの確率を確認しました。
s[s > 0].count() / s.count()
結果です。
0.4973
表が出た確率は 49.7% だったみたいです。 折れ線グラフではプラス側で終わっていたので少し偏りがあったみたいです。 でも 50% に近いので等しい確率で上下していると言っていいと思っています。
ランダムなデータ
ラジオから聞こえてくるザーという雑音のように、市場価格の変化は無意味で特徴のないものだと想定したのです。
正規分布のグラフを作りたかったので変動もランダムなデータで確認してみます。
ランダムなデータを作りました。 サイズは 10000 にしました。
s11 = pd.Series(np.random.randn(10000))
ランダムに作ったデータを積み上げて s12 にしました。
米ドル円のレートをイメージして 110 円から始まるようにしました。
そしてそれを折れ線グラフで表示しました。
s12 = s11.cumsum() + 110
s12.plot()
結果です。
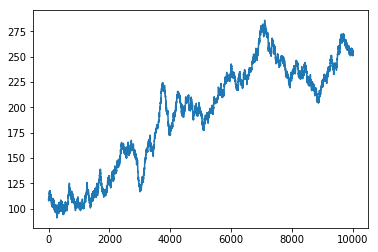
ランダムに作ったデータ s11 の分布を表示しました。
n, bins, patches = plt.hist(s11, 50)
plt.show()
結果です。
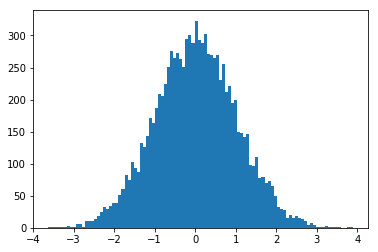
正規分布ぽいグラフができたと思います。
終わり
正規分布のグラフが作れたので今回はこれで終わりにします。
Gist に Jupyter Notebook をアップしておきました。
9 June 2018 追記
次の記事を書きました。